Korean Reasoning Model
Training an o1-like large language model capable of reasoning and responding in Korean.
Contents
Summary
Recently, models equipped with reasoning capabilities have demonstrated remarkable performance, such as ChatGPT-o1.
In the open research community, Deepseek-AI provides recipes for building o1-like models, paving the way to equip models with reasoning capabilities.
Similarly, using the verl repository, we train a large language model that generates its own reasoning process to improve performance. In particular, unlike the open o1-like models that support only English responses, we align our model to generate both reasoning traces and final summaries (i.e., primarily tokens without mathematical notation or code) in Korean.
We achieve performance improvements of up to 18.67% points over the original model, despite constraints on language consistency.
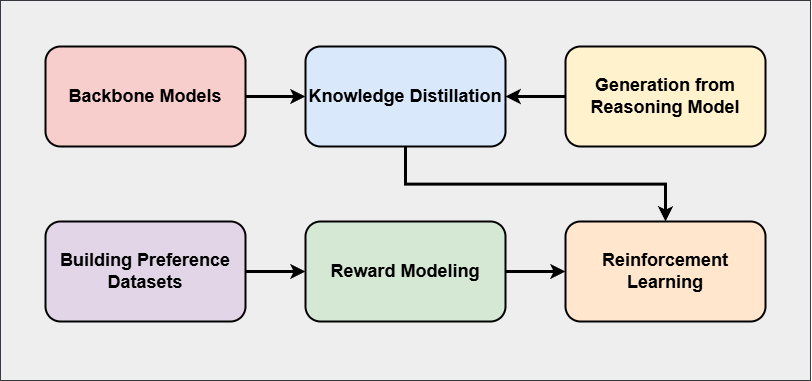
Training Pipeline
-
Building Datasets
-
Knowledge Distillation
-
Reward Modeling
-
Reinforcement Learning
Building Datasets
Following previous research, we generate prompt-response pairs for math and general conversation from a high-capability reasoning model for the knowledge distillation stage.
We generate responses to the same prompts from multiple models. In addition, we improve the quality of the data through outcome-based filtering and generative rewards, collecting approximately 200k data samples for knowledge distillation process.
Knowledge Distillation
We train the model to generate reasoning trajectories using Qwen2.5-1.5B-Instruct for this work. This model is chosen due to its strong performance in both Korean and English, as well as its permissive commercial use.
Using the prompt-response pairs generated in the previous stage, we perform black-box distillation, which enable the model to learn how to generate thoughts from cold-start data.
Reward Modeling
To assign rewards for general conversation, we build a reward model that supports Korean. This process mainly follows the pipeline of Skyword-Reward, and we use publicly available models that support Korean to generate Korean response (chosen, rejected) pairs (e.g., Mistral, Qwen).
Based on the generated responses, we assign rewards using three open reward models. After performing re-centering based on the performance of each model, we construct three types of preference datasets (chosen, rejected pairs).
We train the reward model using each type of dataset, and select the final model by evaluating its performance on RewardBench and Multilingual Reward Bench.
Reinforcement Learning
At this stage, our goal is to endow the chat model obtained from the knowledge distillation phase with reasoning capability. Specifically, we train the model on math data using outcome-based rewards, which have been shown in previous studies to contribute significantly to performance improvement. Similar to Deepseekai-R1, we apply the reward model to summaries only.
Unlike previous successful reproductions, we additionally apply a language consistency reward, focusing on aligning the language used between the input prompt and the generated thought. One of the key insights from this process is that removing code snippets, mathematical equations, and markdown elements is crucial for preventing reward hacking.
We are able to accomplish this task by applying the GRPO reinforcement learning method.
Results
In this section, we present the performance evaluation of the trained reward model and the fine-tuned final reasoner on the reward benchmark datasets and mathematical datasets, respectively.
Reward Model
| Models | Chat | Chat Hard | Safety | Reasoning | Overall | w/o Reasoning | M-Reward Bench |
|---|---|---|---|---|---|---|---|
| GPT-4o-0513 | 96.60% | 70.40% | 86.70% | 84.90% | 85.37% | 85.98% | - |
| GPT-4o-0806 | 96.10% | 76.10% | 88.10% | 86.60% | 87.12% | 87.80% | - |
| GPT-4o-1120 | 95.80% | 71.30% | 86.20% | 85.20% | 85.41% | 85.71% | - |
| Claude-3.5-sonnet-0620 | 96.40% | 74.00% | 81.60% | 84.70% | 84.58% | 84.48% | - |
| Claude-3.5-sonnet-1022 | 96.40% | 79.70% | 91.10% | 87.60% | 88.70% | 90.09% | - |
| DeepSeek-V3 | 96.90% | 79.80% | 87.00% | 84.30% | 86.15% | 88.43% | - |
| GPT-4 Turbo | - | - | - | - | - | - | 82.50% |
| GPT-4o | - | - | - | - | - | - | 79.20% |
| Nemotron-4-340B-Reward | 95.80% | 87.10% | 91.50% | 93.70% | 92.83% | 91.83% | - |
| Gemini-1.5-Pro-0514 | 92.30% | 80.60% | 87.50% | 92.00% | 89.90% | 87.39% | - |
| Meta-Llama-3-70B-Instruct-Self-Taught | 98.00% | 80.30% | 90.50% | 82.20% | 85.91% | 90.46% | - |
| Meta-Llama-3-70B-RM-Helpsteer2-classifier | 91.30% | 80.30% | 92.80% | 90.70% | 90.08% | 89.38% | - |
| Ours (w. Reasoning) | 75.14% | 87.94% | 91.62% | 91.99% | 88.94% | 85.55% | 84.04% |
| Ours (w.o Reasoning) | 94.13% | 81.58% | 91.89% | 78.33% | 86.47% | 90.17% | 84.66% |
The performance table shows a linear positive correlation between model size and reward benchmark performance. Additionally, while closed-source LLMs demonstrate excellent reward performance, there are significant limitations to using them for training. Nevertheless, we observe that the reward benchmark performance for the Korean language remains insufficient. In contrast, our model demonstrates balanced performance in both English and Korean.
We note that rewards related to reasoning are excluded from the reward model training data to enable the application of rule-based rewards. In fact, during our experiments, we find that models with high performance in reasoning tended to show relatively lower results in general conversation and multilingual rewarding tasks.
Math
| Models | AIME 2024 | AMC 2023 | AMC-ko |
|---|---|---|---|
| Qwen/Qwen2.5-1.5B-Instruct | 0.0% | 25.75% | 6.02% |
| DeepSeek-R1-Distill-Qwen-1.5B (Think in English) | 20.67% | 45.75% | 37.34% |
| Ours | 18.67% | 35.00% | 25.63% |
To evaluate the reasoning capabilities of our model, we utilize benchmark datasets AIME2024 and AME2023. We adopt pass@1 as the evaluation metric, and the baselines for comparison included the Qwen/Qwen2.5-1.5B-Instruct and DeepSeek-R1-Distill-Qwen-1.5B models.
Our fine-tuned model demonstrates the highest performance, showing a remarkable improvement over the base model Qwen/Qwen2.5-1.5B-Instruct, particularly on the AIME2024 dataset. Furthermore, it achieve performance comparable to that of the DeepSeek-R1-Distill-Qwen-1.5B model. Importantly, unlike the English-only baselines, our model supports reasoning in Korean, which retains significant value.
On the Korean-translated AMC2022 and AMC2023 datasets, the Qwen model exhibits limited reasoning ability and achieves low performance. In contrast, DeepSeek model, which is primarily trained on Chinese and English, shows notable performance but is unable to generate responses in Korean. Our model, however, supports Korean input and achieves the compable performance among the models tested. However, it is also capable of generating responses in Korean. Furthermore, a performance gap remains when compared to English inputs, indicating room for further improvement.
Examples
---
### English
Prompt:
Alice and Bob play the following game. A stack of $n$ tokens lies before them. The players take turns with Alice going first. On each turn, the player removes either $1$ token or $4$ tokens from the stack. Whoever removes the last token wins. Find the number of positive integers $n$ less than or equal to $2024$ for which there exists a strategy for Bob that guarantees that Bob will win the game regardless of Alice's play.
Response:
<think>Okay, so Alice and Bob are playing this game with a stack of n tokens. They take turns removing either 1 or 4 tokens. Alice goes first. The person who takes the last token wins. I need to find how many positive integers n ≤ 2024 allow Bob to have a winning strategy, no matter what Alice does. Hmm, let's see.\n\nFirst, this seems like a combinatorial game theory problem. I remember that in such games, we often look for winning and losing positions.
...
**Numbers congruent to 0 modulo 5**: These are \\( 5, 10, 15, \\ldots, 2020 \\). The number of such terms is \\( \\left\\lfloor \\frac{2024}{5} \\right\\rfloor = 404 \\).\n2. **Numbers congruent to 2 modulo 5**: These are \\( 2, 7, 12, \\ldots, 2022 \\). The number of such terms is \\( \\left\\lfloor \\frac{2024 - 2}{5} \\right\\rfloor + 1 = 405 \\).\n\nAdding these together, the total number of losing positions is \\( 404 + 405 = 809 \\).\n\nThus, the number of positive integers \\( n \\leq 2024 \\) for which Bob can guarantee a win is \\(\\boxed{809}\\)."
---
---
### Korean
Prompt:
너는 지금 게임을 하고 있어. $3 imes 3$ 격자판 위에 $2 imes 1$ 직사각형이 인접한 두 칸을 (가로거나 세로로) 덮고 있는데, 어떤 두 칸이 덮였는지는 알려주지 않아. 네 목표는 직사각형이 덮고 있는 칸 중 하나라도 찾아내는 거야. "한 번의 시도"는 네가 어떤 칸을 찍는 걸 의미하고, 찍고 나면 그 칸이 숨겨진 직사각형에 덮여 있는지 알려줘. 직사각형이 덮고 있는 칸 하나를 무조건 찾아내려면 최소 몇 번을 찍어야 할까?
Response:
좋아, 이 문제를 풀어보자. 문제는 3x3 격자판 위에 2x1 직사각형이 인접한 두 칸을 덮고 있는데, 어떤 두 칸이 덮였는지도 모르니까, 네가 특정 칸을 찍으면 그 칸이 직사각형에 덮여 있는지 확인해야 해. 그리고 이걸 하기 위해 최소 몇 번의 시도가 필요할까?
먼저, 3x3 격자판의 전체 칸 수를 생각해보자. 3x3은 9개의 칸이 있겠지. 직사각형은 2x1이니까, 가로로는 3칸, 세로로는 1칸을 차지하겠지.
...
2. **시도 방법**: - 각 칸을 순회하며, 네가 해당 칸을 찍으면 직사각형이 덮인지 확인한다. - 예를 들어, 첫 번째 시도: \( (1,1) \)을 찍으면 직사각형이 \( (1,1) \)과 \( (1,2) \)를 덮게 된다. - 두 번째 시도: \( (1,2) \)을 찍으면 직사각형이 \( (1,2) \)과 \( (2,2) \)를 덮게 된다. - 세 번째 시도: \( (2,1) \)을 찍으면 직사각형이 \( (2,1) \)과 \( (2,2) \)를 덮게 된다. - 네 번째 시도: \( (2,2) \)을 찍으면 직사각형이 \( (2,2) \)와 \( (3,2) \)를 덮게 된다.
3. **검증**:
- 이러한 시도 방법을 통해 모든 가능한 직사각형 위치를 검토할 수 있다.
- 따라서, 최소 4번의 시도가 필요하다.
### 최종 답
\boxed{4}
---
Discussion
During the course of the project, we derive the following N insights. Furthermore, techniques aim at enhancing reasoning capabilities, which emerges during the project, have been internalized as proprietary assets within the corporate.
- Utilizing overly difficult samples during the knowledge distillation phase can lead to performance degradation. This phenomenon is closely related to the capability of the backbone model.
- For instance, the model trained on data distilled from
Qwen2.5-1.5B-Math-Instructdemonstrates superior performance on mathematical benchmarks.
- For instance, the model trained on data distilled from
-
Applying rule-based rewards through formatting reward functions initially leads to a
reduction in the number of generated tokens, as the model prioritizes preserving the target format duringearly training stages. This trend gradually mitigates over time and is particularly pronounced compared to the model only undergoing knowledge distillation. - When enforcing rules to maintain
language consistency, applying rewardsbased on the proportion of tokensgenerated during the “thinking process” tends to suppress the generation of mathematical equations or code blocks.- Even subtle differences in reward can lead to
reward hacking, causing the model to converge on trivial solutions. - This issue can arise even in the absence of ratio-based rewards if there is no rule to explicitly disregard equations or code blocks.
- Even subtle differences in reward can lead to
- During reward model training, the presence or absence of reasoning data significantly impacts performance on general conversation tasks.
- This phenomenon may indicate a limitation tied to the size of the reward model, warranting further investigation.
- In this project, rule-based rewards were applied to reasoning data (mathematics), and the reward model was trained excluding these samples.
-
A greater number of rollouts per queryand larger batch sizes are effective forimproving modelperformance and accelerating training.- Samples that are either too easy (i.e., correct answers across all rollouts for a given query) or too difficult (i.e., incorrect answers across all rollouts) do not contribute meaningfully to learning.
- Samples that are appropriately challenging—where the model can occasionally produce the correct answer within certain episodes—contribute significantly to performance improvements.