Knowledge Distillation
Transferring the capabilities of a large language model to a smaller one.
Contents
Summary
Recent efforts have focused on training foundation models more efficiently and effectively. To this end, both classical approaches such as knowledge distillation and more sophisticated techniques have been explored. For example, Gemma 3 was distilled from Gemini usning thier improved approach (GKD), and the LLaMA series also maximized training efficiency through distillation from larger models. Particularly, as the importance of reasoning models has grown, this approach has been adopted in models like Qwen3 and DeepSeek, demonstrating its effectiveness.
Knowledge Distillation, initially developed for vision models, has proven effective for language models as well. In the era of large language models (LLMs), two main types of distillation have emerged: white-box and black-box. Among these, white-box distillation is applicable when the teacher model’s logits are observable. This method has recently evolved in close connection with reinforcement learning [1, 2, 3].
Despite these advances, existing methods still operate under the strong-to-weak distillation paradigm. We observe that there remains significant room for improvement. Inspired by the concept of Weak-to-Strong Generalization, we propose a new approach that leverages additional signals from weak models to further enhance performance.
Our method introduces a framework in which feedback is generated from a weaker model of the same size. Rather than treating this feedback as reliable supervision, we treat it as noisy or incorrect information and train the model accordingly. This allows the learning process to benefit from diverse and challenging signals.
Our approach achieves over 3% improvement compared to existing state-of-the-art models and shows superior performance on 4 out of 5 benchmarks.
Methodology
-
Overview
-
Learning from teacher
-
Training the classmate
-
Learning from strong and weak model
Overview
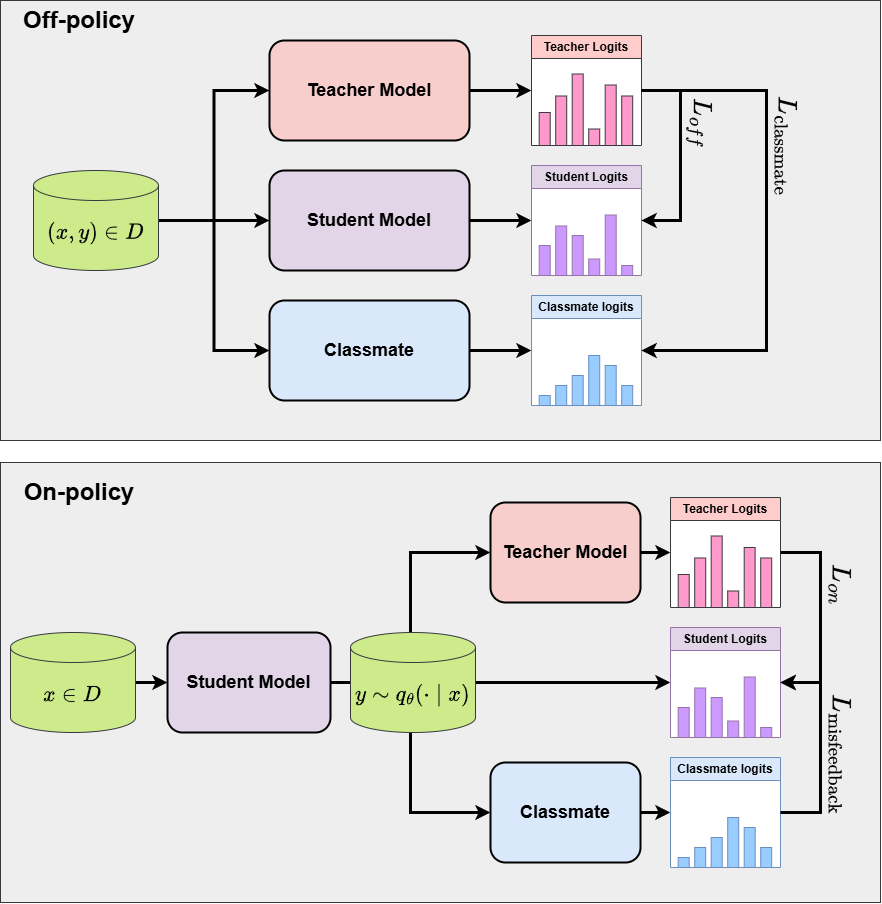
We propose a novel learning approach that not only facilitates knowledge transfer from a strong model (referred to as the teacher) but also leverages models that are smaller or exhibit lower performance than the target model (referred to as the student) to enhance performance.
We conceptualize this learning mechanism as analogous to how a student acquires knowledge in a classroom setting—not only from a teacher but also from peers—thus, we term this approach class knowledge distillation. In this context, the lower-performing models are referred to as classmate models.
Our method employs an RL-like approach, where feedback is received from the teacher based on sentences generated in an on-policy manner. Simultaneously, feedback is also obtained from classmate models; however, this feedback is regarded as potentially incorrect and is therefore termed misfeedback. The learning objective is to diverge from the sentence distribution of the classmate models while converging towards that of the teacher, following a paradigm similar to contrastive learning.
Learning from teacher
We conduct training using a fixed instruction-following dataset $(x, y) \in \mathcal{D}$, where $x$ denotes a user prompt and $y$ denotes the corresponding assistant response.
Training is performed using a static dataset by computing token-level logits from both a teacher model and a student model, and minimizing the Kullback–Leibler divergence between their output distributions (off-policy distillation). This process can be formulated as follows:
To mitigate the training–inference mismatch, also known as exposure bias, we further incorporate student-generated outputs (SGO) into the training process. In this setting—analogous to on-policy training in reinforcement learning—the student model generates a response for a given prompt, and distillation is performed using the teacher model’s logits corresponding to the generated sequence. The procedure can be expressed as:
In this context, it is important to note that the choice of loss function can have a significant impact on model performance.
Training the classmate
In addition to training the student model, we simultaneously train a classmate model. Since a poorly trained classmate may provide low-quality or misleading feedback (i.e., misfeedback), leading to meaningless learning signals, we adopt a training strategy that allows the classmate to gradually improve over time.
Notably, our empirical results suggest that the degree to which the classmate is trained plays a crucial role in achieving effective weak-to-strong generalization. Furthermore, the ability to precisely control the training dynamics of the classmate is a key factor in maximizing the effectiveness of our proposed framework.
The classmate is trained under a loss function analogous to that used for the student model. However, the classmate’s generated samples are not used for training. Instead, it learns solely from the teacher’s supervision. This design choice is made to prevent the classmate from becoming overly dominant in performance.
The objective function for the classmate model is defined as:
\[L_{\text{classmate}}(p, c_\phi) = \mathbb{E}_{x \sim D} \left[ \mathbb{E}_{\mathbf{y} \sim p(\cdot|\mathbf{x})} \left[ \log \frac{p(\mathbf{y}|\mathbf{x})}{c_\phi(\mathbf{y}|\mathbf{x})} \right] \right]\]where $c_\phi$ denotes the classmate model parameterized by $\phi$.
Learning from weak models
We propose a learning approach in which the student model is trained using feedback from a classmate model that performs worse than the student, but not to the extent of significantly underperforming. This setup bears resemblance to contrastive learning objectives or Direct Preference Optimization (DPO).
Intuitively, during student-generated output (SGO) training, the classmate provides feedback in a manner analogous to the teacher model. However, instead of directly following this feedback, the student is trained to resist or apart from the misfeedback provided by the classmate.
This training paradigm can be viewed as analogous to DPO, where the objective is to decrease the likelihood of generating rejected samples. Similarly, it aligns with the principle of contrastive learning, where representations are encouraged to move away from negative samples in the latent space — or, in our context, the sentence space.
\[L_{\text{misfeedback}}(q_\theta, c) = - \mathbb{E}_{x \sim D} \left[ \mathbb{E}_{\mathbf{y} \sim q_\theta(\cdot|\mathbf{x})} \left[ \log \frac{q_\theta(\mathbf{y}|\mathbf{x})}{c(\mathbf{y}|\mathbf{x})} \right]\right]\]Performance Comparisons
| Models | Dolly | Self-inst | Vicuna | Super-Natural | Unnatural | AVG |
|---|---|---|---|---|---|---|
| GKD | 23.75 | 12.73 | 16.64 | 26.05 | 27.70 | 21.37 |
| MiniLLM | 23.84 | 12.44 | 18.29 | 22.62 | 23.26 | 20.09 |
| DistiLLM | 26.11 | 13.14 | 18.46 | 27.51 | 30.11 | 23.07 |
| Ours | 27.02 | 13.68 | 17.41 | 28.51 | 30.26 | 23.38 |
We conduct a comparative evaluation of our CKD method against several state-of-the-art distillation techniques on five benchmark datasets.
- Dolly: the 500-sample test set we split from the databricks-dolly-15k dataset.
- Self-inst: A user-oriented instruction-following set with 252 samples.
- Vicuna: The 80 challenging questions used in the Vicuna evaluation.
- Super-Natural: : The test set of SUPER-NATURALINSTRUCTIONS consisting of 9K samples ranging from 119 tasks.
- Unnatural: We randomly sample 10K samples from the core set of UNNATURALINSTRUCTIONS for evaluation.
We adopt the Rouge-L score to evaluate the model-generated response.
Firstly, we observed that our knowledge distillation method achieved the highest performance across all datasets, with the exception of a single benchmark.
Although our model was trained solely on the Dolly training dataset, its consistently strong performance across diverse datasets demonstrates its robust generalization ability.
At the same time, our findings provide evidence that weak-to-strong generalization is also applicable in the context of knowledge distillation. To the best of our knowledge, this is the first such observation reported at the sentence level in knowledge distillation.
Moreover, it is important to note that all other models perform distillation from supervised fine-tuned models, meaning that our method does not incur a significant increase in computational budget.
Notably, the baseline methods considered are orthogonal to our training framework. As such, ideas from approaches like MiniLLM and DistiLLM can be incorporated into our framework, potentially leading to further improvements in performance.
Discussion
This work is part of an ongoing project and is subject to continuous updates and revisions. Furthermore, we note that the approach is intended for internal use within a corporate aimed at building compact yet powerful models, and is not intended for external release.
- We deviate from the traditional strong-to-weak knowledge distillation paradigm and observe that
weak-to-strong distillationcan effectively improve model performance.- This phenomenon can be interpreted similarly to contrastive learning, suggesting that negative samples or negative feedback may serve as valuable learning signals.
- In particular, we find that the effectiveness of negative samples is highly sensitive to their difficulty:
overly easy (easy negatives) or overly hard (hard negatives) samples can adversely affect training. Careful control over this difficulty is therefore crucial.
- We also observe that leveraging SGO during training significantly contributes to performance improvements. Notably, even when pool samples are generated in early epochs, meaningful learning signals can still be extracted through the use of classmate models.
- This suggests a potential advantage over methods such as DistiLLM or MiniLLM, which aim to mitigate the negative impact of low-quality samples generated in early training stages. Our findings indicate that such early samples may instead offer opportunities for improvement when properly utilized.